- Autora admin carl@lifeloveeveryday.com.
- Public 2023-12-16 19:18.
- Última modificació 2025-01-23 15:29.

Exemples de la proporció àuria es poden trobar a tot arreu a l'arquitectura clàssica, obres d'art, natura i fins i tot música. Aquesta expressió de proporció, també coneguda com a Ratio Divina, ofereix una composició harmònica mitjançant l'aplicació d'un nombre irracional (1.618) en el disseny, tant natural com fet per l'home. El més probable és que desconeixeu les matemàtiques que hi ha darrere de la bellesa de la proporció àuria perquè produeix objectes i música que naturalment us agradaran sense necessitat de cap explicació.
Proporció Àurea a l'Arquitectura
La proporció daurada crea una bellesa gairebé perfecta a la natura i l'art. Quan comenceu a buscar exemples de la proporció àuria a la vida quotidiana, potser us sorprendran els molts casos en què s'ha utilitzat per crear molts edificis i estructures monumentals. Quan s'utilitza la proporció àuria en arquitectura, es diu que l'edifici es crea utilitzant "arquitectura sagrada". Aplicant el càlcul de la proporció àuria a un quadrat, els arquitectes i els dissenyadors són capaços de crear el rectangle daurat, que es creu que té les proporcions més agradables estèticament per a l'ull humà.
Rectangle daurat Exemple: El Partenó

Fídies, l'escultor grec, va utilitzar la proporció àuria en la seva obra, sobretot quan va començar a treballar amb les bandes que va esculpir just a sobre de les columnes del Partenó. També és important tenir en compte que el valor numèric assignat a la proporció àuria, Phi, va ser nomenat en el seu honor.
Si mesureu les dimensions de l'exterior del Partenó, descobrireu que no només forma un rectangle daurat, sinó que també hi ha molts rectangles daurats entre les columnes. Aquesta estructura sagrada és un bell exemple de la proporció àuria en arquitectura.
Triangle d'Or Exemple: Gran Piràmide de Gizeh
La proporció d'or, el rectangle d'or i el triangle d'or es poden trobar a la perfecció d'una de les Set Meravelles del Món, la Gran Piràmide de Gizeh. Per trobar la proporció àuria, haureu de reduir a la meitat la base quadrada de la piràmide i dibuixar una línia vertical al centre de la piràmide. Quan es connecta a un costat angulat de la piràmide, podeu veure fàcilment com forma el Triangle daurat amb una proporció de 1,618, la proporció daurada.
Altres exemples arquitectònics
Podeu trobar molts exemples d'arquitectura sagrada de l'antiga a la moderna i edificis de la proporció àuria.
- Catedral de Chartres - Centre, França
- Notre Dame - París, França
- Porch of Maidens - Acròpolis, Atenes
- Taj Mahal - Agra, Índia
- Edifici de les Nacions Unides - Nova York, Nova York
Proporció daurada en exemples d'art
Podeu trobar molts exemples de mestres pintors que van utilitzar la proporció àuria. Aquestes obres de perfecció es van crear utilitzant la proporció de rectangles d'or i triangles d'or. L'art creat a partir del rectangle daurat demostra ser més agradable a l'ull humà. És un dels misteris que envolta aquest rectangle perfecte i la proporció àuria.
Proporció àurea en l'art

Els exemples d'art de la proporció d'or inclouen:
- Leonardo Di Vinci - Mona Lisa, home de Vitruvi
- Botticelli - Naixement de Venus
- Miquel Àngel - Sagrada Família, 'David'
- Raphael - Crucifixió
- Rembrandt - Autoretrat
- Salvador Dalí - El sagrament de l'últim sopar, la persistència de la memòria
Ús de la proporció àuria en la composició artística
Dins d'un rectangle daurat hi ha certes àrees que es troben més atractives visualment que altres àrees. Aquests punts es descobreixen dibuixant una línia des de la cantonada inferior del rectangle fins a la cantonada oposada i repetint-la amb l' altra cantonada inferior. Aquestes línies es tallaran al centre exacte del rectangle daurat. A continuació, mesura el mig camí al llarg de cada línia començant des del punt central. Aquests quatre punts s'anomenen els ulls del rectangle (proporció d'or). El punt focal principal de la pintura es dibuixa o pinta dins d'aquests punts d'interès (ràtios).
Proporció d'or a la música

La música es compon de valor numèric i quan s'utilitza la proporció àuria per crear una peça musical, es converteix en un exemple viu de matemàtiques. La seqüència de Fibonacci també predomina a la música:
- Hi ha vuit notes en una escala.
- La tercera i la cinquena notes són la base dels acords.
- La longitud, o octava, de qualsevol nota és de 13 notes.
La seqüenciació continua al llarg d'una peça musical i es fa més complexa a mesura que assoleix la proporció daurada.
Compositors que van utilitzar la proporció àuria
Alguns dels compositors clàssics més coneguts van utilitzar la proporció àuria i la seqüenciació de Fibonacci en les seves peces musicals, com Bach, Beethoven, Chopin i Mozart. Alguns compositors moderns com Casey Mongoven han explorat la proporció àuria a la seva música.
Exemples de proporció d'or a la natura

On es troba la proporció àuria a la natura? Es troba a l'espiral daurada o de Fibonacci, que es pot crear utilitzant la proporció àuria. Aquest és un fenomen que es troba àmpliament al món natural. Les fulles d'una planta creixen perquè el màxim possible puguin pujar en espiral per la tija. Una nova fulla només es forma després de la que s'ha format.
- Cactus en espiral
- Gàxies espirals
- Giras-sols
Flors amb la seqüència de Fibonacci
Algunes flors tenen pètals de flors que segueixen la seqüència de Fibonacci:
- Tres pètals:Iris, lliri, orquídies, trillium
- Cinc pètals: Ranuncles, geranis, hibisc, glòria matinal, caputxins
- Vuit pètals: Delphiniums
- 13 pètals: Algunes varietats de margarides, herba canya, calèndula
Espiral de Fibonacci en pinyes

Depenent de l'espècie d'arbre, també podeu veure la proporció àuria en funcionament dins d'una sèrie de números de Fibonacci en pinyes. Podeu trobar una sèrie de vuit espirals a un costat de la pinya, amb 13 espirals a l' altre. Un altre patró de pinya té cinc espirals a un costat i vuit a l' altre.
Proporció àurea en humans
Aquesta proporció també és important no només per a com es veuen els humans, sinó també pel que fa al funcionament del seu cos i en el seu ADN.
L'ADN revela la proporció àuria
Un dels exemples més sorprenents de la proporció àuria es troba dins de l'estructura de l'ADN humà. Això es pot veure en una única secció transversal d'ADN que revela que la doble hèlix d'ADN forma una forma de decàgon. Aquesta és una combinació de dos pentàgons, girats 36 graus l'un de l' altre, forma la doble hèlix d'ADN. L'espiral de la doble hèlix forma un pentàgon. Fins i tot una sola molècula d'ADN revela una base de la Secció Àurea o Proporció Divina.
Les matemàtiques darrere de la proporció àuria
Trobar la proporció àuria a la vida real és senzill, ja que apareix al teu voltant. És un truisme matemàtic que s'utilitza per definir el que es coneix comunament com el nombre perfecte que es troba a la natura que ha estat duplicat i imitat pels humans durant segles. La bellesa simplista d'aquest número dissimula la seva complexitat en l'execució. Per entendre la teoria darrere de la proporció àuria, primer heu d'explorar la seqüenciació de Fibonacci de la proporció.
Seqüència de Fibonacci i la proporció àuria
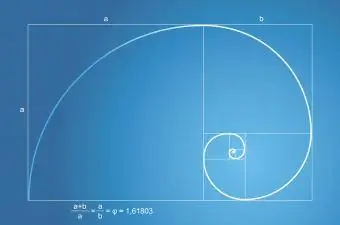
La seqüència o sèrie de Fibonacci té una relació amb la proporció àuria. La sèrie de Fibonacci es mostra en el nombre de fulles d'una planta i en el nombre de pètals d'una flor. L'espiral de Fibonacci, que es troba a la natura, sempre forma part d'un rectangle daurat amb una proporció daurada.
Les matemàtiques de la sèrie de Fibonacci són senzilles:
- La seqüència comença amb 0 i 1.
- Només sumeu els dos últims números per obtenir el següent número de la sèrie.
- 0+1=1, 1+1=2, 1+2=3, 2+3=5, 3+5=8, i així successivament.
- Aquest exemple de la sèrie de Fibonacci es converteix en: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, i així successivament.
La relació de Fibonacci amb la proporció àuria es realitza quan s'afegeix cap endavant, més i més. Com més afegiu la sèrie, més us acosteu a la proporció àuria.
Creació d'un rectangle i un triangle daurat
Per crear un rectangle daurat amb la seqüència de Fibonacci, comenceu amb un quadrat. Començareu a construir un rectangle afegint un altre quadrat al quadrat original. Recordeu utilitzar la fórmula: 0+1=1 és el primer quadrat, 1+1=2 - afegireu un altre quadrat.1+2=3 afegireu tres quadrats i, a continuació, 2+3=5, afegireu cinc quadrats. Continuareu afegint quadrats i, finalment, formareu un rectangle daurat.
Es pot crear un triangle daurat dividint un rectangle daurat d'una cantonada a la cantonada oposada. Això crea un triangle on els seus tres costats o angles tenen una proporció de 2:2:1, és a dir, els dos costats llargs tenen la mateixa longitud i l'angle curt és exactament la meitat de la longitud dels dos més llargs.
Proporció d'or al món real
La proporció daurada es coneix sovint com la proporció divina a causa de la seva importància a la natura i als cossos humans. El descobriment que la proporció àuria està present en tants éssers vius va fomentar una reverència per aquesta proporció màgica, i continua sent una inspiració per als artistes i creadors d'avui.






